Руслан Хазарзар

Апории Зенона

Τὸ κιωούμενον οὔτ’ ἐν ᾧ ἐστι τόπῳ κινεῖται οὔτ’ ἐν ᾧ μὴ ἔστι.

Ζηνων Ελεατης

То, что движется, не движется ни в том месте, где оно есть, ни в том, где его нет.

Зенон Элейский

Ad notam

Как показывает мой личный опыт, апории Зенона — идеальный тест на самостоятельность мышления. Причем это — тот самый тест, на котором могут «завалиться» люди с самыми почетными званиями. Мало того, его, как правило, не проходят именно обладатели технических дипломов и степеней, называя Зенона софистом. Потому что «технари» привыкли оперировать четкими определениями, установленной формализацией и т. д. А апории Зенона — это тот самый гносеологический кошмар, который зрит в самый корень и ставит под сомнение любую формализацию и любые термины. Они требуют мышления, не отягощенного догмами, т. е. самостоятельного мышления. Они показывают разницу между знаниями и разумом, начитанностью и умом.

Апории Зенона неразрешены и поныне. Причем современные издания, в отличие от советских, с этим соглашаются: «А[пории] теперь признаются подлинными парадоксами, связанными, в частности, с описанием движения»[1]. Как вы увидите в дальнейшем, все т. н. «разрешения» апорий представляют собой логическую ошибку ignorantia elenchi, состоящую в том, что доказывается не тот тезис, который требуется доказать.

Разумеется, мало сказать, что апории неразрешимы. Мы рассмотрим, какие глобальные вопросы выросли из незамысловатых апорий. Оказалось, что ни математика, ни физика, ни другая наука не могут обезвредить элеатских парадоксов. Наоборот, сами апории и вытекающие из них вопросы постоянно требуют пересмотра уже устоявшейся формализации. И для разрешения апорий необходимо разрешить основополагающие вопросы: чтó собой представляет мироздание — бытие или становление? чтó такое бесконечность? дискретен мир или непрерывен? как разрешить проблемы пространства и времени? и т. д.

Формулировки апорий Зенона дошли до нас через «Физику» Аристотеля. Нельзя назвать эти формулировки удовлетворительными, и потребность в их пересмотре наблюдалась еще в древности. Так, Темистий (IV в.), Симпликий (VI в.) и Иоанн Филопон (VI в.) в своих комментариях на Аристотелеву «Физику» пытались переформулировать или уточнить аргументы Зенона. Дело в том, что Аристотель, «разрешая» апории, то ли не понял, то ли не захотел понять всю полноту проблем, следующих из аргументов Зенона. Однако я не ставил перед собой задачи реконструировать зеноновские аргументы, я предлагаю лишь понять, на какие трудности в анализе движения указал Зенон Элейский. Именно указал, поскольку о попытке приписать непосредственно Зенону современную постановку проблем движения не может быть и речи. Кстати говоря, эта постановка в логико-философской литературе не отличается единством. Нередко ответственность за парадоксы движения возлагается на неточность и размытость используемых понятий[2]. Мол, уточним понятия — парадоксы исчезнут. Я с этим не могу согласиться: апории Зенона касаются самих основ человеческого миропонимания; они требуют не просто уточнения понятий, а выбора философской платформы объяснения действительности. А поскольку дело построения таких платформ не может быть завершено, пока существует мыслящий разум, на выборе одной из них лежит печать неизбежной исторической ограниченности. Причем сказанное в полной мере относится и к нижеприведенным построениям.

Аргумент к непрерывности

Как известно, Зенон сформулировал четыре апории против движения. Свое исследование мы начнем с первых двух апорий, касающихся непрерывности пространства-времени. Прежде всего обратимся к «Физике» Аристотеля (Aristoteles. Physica. Z, 9).

[Διχοτομία]

τέτταρες δ’ εἰσὶν οἱ λόγοι περὶ κινήσεως Ζήνωνος οἱ παρέχοντες τὰς δυσκολίας τοῖς λύουσιν, πρῶτος μὲν ὁ περὶ τοῦ μὴ κινεῖσθαι διὰ τὸ πρότερον εἰς τὸ ἥμισυ δεῖν ἀφικέσθαι τὸ φερόμενον ἢ πρὸς τὸ τέλος.

Дихотомия

«Есть четыре аргумента (λόγοι) Зенона о движении, которые доставляют трудности тем, кто пытается их разрешить. Первый — о невозможности движения, так как перемещающееся [тело] прежде должно дойти до половины, нежели до конца» (239b, 9-13).

[Ἀχιλλεύς]

δεύτερος δ’ ὁ καλούμενος Ἀχιλλεύς· ἔστι δ’ οὗτος, ὅτι τὸ βραδύτατον οὐδέποτε καταληφθήσεται θέον ὑπὸ τοῦ ταχίστου· ἔμπροσθεν γὰρ ἀναγκαῖον ἐλθεῖν τὸ διῶκον ὅθεν ὥρμησεν τὸ φεῦγον, ὥστε ἀεί τι προέχειν ἀναγκαῖον τὸ βραδύτερον.

Ахиллес

«Второй [аргумент] — так называемый «Ахиллес». Он гласит, что медленного [бегуна] никогда (οὐδέποτε) не догонит быстрый [бегун], ибо необходимо, чтобы догоняющий прежде достиг [той точки], откуда стартовал (ὥρμησεν) убегающий, поэтому более медленный [бегун] по необходимости всегда должен быть чуть впереди» (239b, 14-18).

Обратимся прежде к апории «Ахиллес», суть которой восходит к сцене, изложенной в гомеровской «Илиаде»: Ахиллес гонится за Гектором и останавливается, так и не догнав быстроногого врага. А если бы Ахиллес гнался не за быстроногим Гектором, а за тихоходной черепахой? Так вот, согласно апории, Ахиллесу ни за что не догнать черепаху. Аргументы апории сводятся к тому, что, когда преследующий достигнет места, где находился преследуемый в момент старта, догоняемый бегун продвинется, хотя и немного, дальше. Значит, на новом небольшом участочке пути Ахиллесу снова придется догонять черепаху. Но пока преследователь добежит до этого второго пункта, беглянка снова переместится вперед. И так далее до бесконечности.

Примем следующие условия. Пусть Ахиллеса отделяет от финиша расстояние 1, а черепаху — ½. Двигаться Ахиллес и черепаха начинают одновременно. Пусть для определенности Ахиллес бежит в 2 раза быстрее черепахи. Тогда, пробежав расстояние ½, Ахилл обнаружит, что черепаха успела за то же время преодолеть отрезок ¼ и по-прежнему находится впереди героя. И т. д.

Знающие математический анализ обычно указывают, что ряд

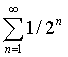
сходится к 1. Поэтому, дескать, Ахиллес преодолеет весь путь за конечный промежуток времени и, безусловно, обгонит черепаху. Действительно, в передаче Аристотеля весьма неопределенно выглядит выражение «никогда (οὐδέποτε) не догонит», и, по всей вероятности, это — интерпретация апории самим Стагиритом, ибо он «разрешает» апорию как раз вышеуказанным образом.

Однако вряд ли следует считать, что сам Зенон не понимал этого, и уж наверняка он обращал внимание совсем на другое. «Никогда не догонит» — не значит бесконечное течение времени. Согласно апориям, и время не превысит своего предела. А парадокс не опровергается его констатацией. Констатацией он как раз утверждается. К сожалению, многих настолько приучили опровергать путем приведения к противоречию, что они и сами противоречия (парадоксы) готовы «опровергать» подобным же образом. Ведь можно переформулировать апорию следующим образом: «Никогда не пройдет одна секунда, ибо когда пройдет полсекунды, останется полсекунды, когда пройдет половина полсекунды (¼), останется ¼ секунды...» и т. д.

Как же действительно опровергается парадокс? Он опровергается демонстрацией того, за счет чего он существует. Т. е. необходимо указать принципиально неверное утверждение в рассуждениях Зенона, а не демонстрировать путем других рассуждений или эмпирики, что Зенон пришел к противоречию — Зенон об этом и сам прекрасно знал и сам же об этом говорил. Наконец, формулировку апории можно изменить, не меняя ее сути проблемы: «Самый быстрый бегун не сможет догнать самого медленного (хотя при этом он не будет прекращать движения), ибо догоняющий должен прежде достичь того места, откуда сдвинулся убегающий, так что более медленный будет впереди».

В то же самое время вышеозначанное рассуждение, что сумма бесконечного числа временных интервалов все-таки сходится и, таким образом, дает конечный промежуток времени, абсолютно не затрагивает один существенно парадоксальный момент, а именно парадокс, заключающийся в том, что некая бесконечная последовательность следующих друг за другом событий, последовательность, завершаемость которой мы не можем себе даже представить (не только физически, но хотя бы в принципе), на самом деле все-таки должна завершиться. Апория не ставит вопрос о пределе и его вычислении, апория спрашивает: как этот предел в принципе возможно достичь?

Суть проблемы заключается в интеграции бесконечного количества частей, а наука — математический анализ, в частности — рассматривает только дифференциацию уже определенной, а значит, и актуализированной бесконечности: целое уже дано и остается только делить — причем, в случае с бесконечно малыми величинами, уже не актуально, а потенциально! (об этом мы еще будем говорить) — его на части; в то время как Зенон задается вопросом, а как это целое из таких частей составить (а уже потом пробовать его делить)? Получается, само решение возможно только при завершении процесса, т. е., по сути, возможно только при актуальной бесконечности, а это — не что иное, как «разрешение» апории путем постулирования наличия решения. При потенциальной бесконечности, т. е. при условиях, заданных Зеноном, апория неразрешима. Но ведь условия, заданные Зеноном, безупречны с точки зрения логики. Посылка может быть либо ложной, либо универсальной. Ложность посылки никто не утверждает. Но если она универсальна, то вывод логически верен, ибо обратное утверждение противоречит универсальности посылки, что абсурдно. А потому утверждение, что ошибка Зенона якобы заключается в том, что предел бесконечной последовательности не является членом этой последовательности, есть не утверждение ошибки Зенона, но как раз его правоты: действительно, предела «догнал» в рассуждениях Зенона не получается. Логически все безупречно.

Другой аргумент против апорий Зенона высказан философом-интуитивистом А. Бергсоном, который считал, что «делить можно вещь, но не акт»[3]. Зенон же, по мнению Бергсона, смешивает процесс движения, каждый акт которого неделим, с бесконечно делимым пространством. Однако вряд ли можно согласиться с Бергсоном. Похоже, для Зенона было несомненным, что движение есть именно процесс. Ведь он говорит не о трудностях введения завершенных в своей данности отрезков пространства, а о немыслимости процесса их прохождения. Либо движение будет описано как процесс, как ряд последовательных операций или действий по осуществлению движения, либо придется признать, что любая попытка такого описания неминуемо ведет к противоречиям, что будет означать логическую невозможность движения.

При рассмотрении проблем, связанных с апорией «Ахиллес», мне однажды пришлось встретиться еще с один аргументом, суть которого сводилась к следующему: «У нас в условии апории произведено деление на бесконечное число частей. Поэтому то, что мы не можем указать, на каком конечном этапе бегун догонит черепаху, не может служить основанием для утверждения о том, что он не догонит ее за бесконечное число этапов. Доказательство от противного здесь не применимо, мы не можем доказать, исходя из посылок, ни справедливость утверждения, ни справедливость отрицания. Кажущееся логичным рассуждение о том, что раз бегун не догоняет черепаху на конечном числе этапов (мы не можем указать конечный этап, на котором он ее догонит), то он не догонит ее и на бесконечном числе, является порочным кругом: доказывается ровно то утверждение, что кладется в основу». Т. е. ставится под сомнение закон исключенного третьего, дающий основание доказательству от противного (что, кстати, само по себе уже ставит рассуждения Зенона в ряд парадоксов). Но ведь аналогичным путем в математике постулируются сходящиеся суммы: никто не может прямым путем доказать того, что они не превысят своего предела, это доказывается от противного. На каждом из этапов Ахиллес не догоняет черепаху, причем число этих этапов потенциально бесконечно. А потому мы не только не можем указать конечный этап, на котором Ахиллес догонит черепаху, мы знаем, что такой этап невозможен, ибо противоречит посылке. И здесь нет никакого порочного круга как логической ошибки, здесь именно «доказывается ровно то утверждение, что кладется в основу». Circulus vitiosus как ошибка возможен при условном допущении посылки, а в апории посылка — бесспорна. При этом всякая логика тавтологична, если верна, и выводит ровно то, что в нее заложили. Т. е. мы снова возвращаемся к тому, с чего и начали: для опровержения апории необходимо опровергнуть посылку, а она-то как раз и неоспорима.

Другой небезынтересный аспект — тривиальность самой апории «Ахиллес»: мол, речь всегда идет о догоняющем Ахиллесе, а догоняющий (потенциальная бесконечность), разумеется, — и не догнал. Но, с другой стороны, если, как в математическом анализе, уже «дано» (актуальная бесконечность), то и говорить не о чем — апория разрешается, фактически, путем постулирования наличия решения. Но такое «решение» не менее тривиально рассуждений Зенона. Беда в том, что тривиальны оба варианта, и выходит, что в обоих случаях мы получаем ровно то, что постулируем. Но нетривиальность данной апории в том, что Зенон показывает невыводимость актуальной бесконечности из потенциальной. В то же самое время из опыта мы знаем, что догоняющий, если он быстрее, становится догнавшим и перегнавшим. И проблема описания движения в апории остается — во всяком случае, до тех пор, пока не будет постулирована дискретность пространства-времени.

Принципиальная незавершаемость данной последовательности следующих друг за другом событий заключается в том, что в ней отсутствует последний элемент. Всякий раз, указав очередной член последовательности, мы можем указать и следующий за ним. Ведь сколько бы мы ни оперировали бы понятием предела, в конце концов мы обязаны признать, что пределом переменной мы называем постоянную величину, к которой переменная неопределенно приближается, никогда ее не достигая. Но то же самое говорил и Зенон, облекая разве что абстрактные математические символы в яркие образы, навеянные мифами. Как бы далеко мы ни шли в последовательной интеграции укорачивающихся «движеньиц» Ахиллеса, мы никогда не получим целиком его пути до встречи с черепахой. Поэтому вывод Зенона о том, что движение из-за необходимости «пересчитать» бесконечное число точек не может закончиться, еще тогда произвел большое впечатление.

На схожих аргументах основывается апория «Дихотомия», утверждающая невозможность начать движение: для того, чтобы пройти весь путь, движущееся тело сначала должно пройти половину пути, но чтобы преодолеть эту половину, надо пройти половину половины и т. д. до бесконечности. Иными словами, при тех же условиях, что и в предыдущем случае, мы будем иметь дело с перевернутым рядом точек: (½)ⁿ, ..., (½)³, (½)², (½)¹. Если в случае апории «Ахиллес» соответствующий ряд не имел последней точки, то в «Дихотомии» этот ряд не имеет первой точки. Следовательно, движение не может начаться. А поскольку, согласно элеатам, движение не только не может закончиться, но и не может начаться, движения нет и быть не может!

Аргумент к дискретности

Проанализировав апории «Дихотомия» и «Ахиллес», мы обнаружим, что обе они опираются на допущение о непрерывности пространства и времени в смысле их бесконечной делимости. Без допущения тезиса о том, что любой пространственный или временнóй интервал можно разделить на меньшие по длине интервалы, обе апории рушатся.

В свое время атомистика Демокрита была реакцией на выпады элейской школы. Демокрит был апостолом атомизма не только в физике, но и в математике, причем обосновывал необходимость атомистического миросозерцания ссылкой не на физические явления, а на чисто математические затруднения, возникающие в том случае, если считать пространство непрерывным. В дозеноновском естествознании все тела считались беспредельно делимыми. Это с одной стороны. А с другой — допускалось, что каждый предмет состоит из бесчисленного множества непротяженных и далее неделимых «телец». На эти-то противоречивые принципы и обрушился Зенон.

В частности, он говорил, что если тело делимо беспредельно, то оно должно быть бесконечно большим. Как бы далеко ни заходило дробление, всякий раз будут получаться протяженные частицы, размеры коих никогда не обратятся в ноль. Поскольку же деление бесконечно, постольку и геометрических «атомов» будет бесчисленное множество. А если так, то сумма бесконечно большого количества протяженных и далее неделимых элементов окажется неизмеримо огромной. Если же, наоборот, точка как предел деления не имеет размеров, то сложение любого, сколь угодно большого количества таких «нулей» никогда не даст протяженного тела.

Аргументы Зенона произвели ошеломляющее впечатление. И наконец, школа Демокрита попыталась восстановить теоретический фундамент геометрии. Она сделала то же, что делали все последующие поколения «опровергателей» Зенона, — отмахнулась от элеатских искушений. Предел делимости материи и пространства был провозглашен сызнова. Так в ответ на сугубо негативную элеатскую критику появилась позитивная платформа, на которой можно было — худо ли, бедно ли — дальше возводить храм математики и механики. Но тут Аристотель взял и торпедировал эту вроде бы конструктивную платформу, провозгласив свой континуум! Что ж, он был по-своему прав: ведь противоречия, подмеченные Зеноном, делали позиции Демокрита очень и очень шаткими.

Так в чем же заключается зеноновская критики? Автор апорий понимал, что первые две апории («Дихотомия» и «Ахиллес») имеют смысл только при допущении нерерывности пространства и времени, а потому привел также аргументы, исходящие из принятия допущения о дискретности пространства и времени, т. е. допущения о существовании элементарных, далее неделимых, длин и времен. Эти аргументы заключены в третьей и четвертой апориях.

Обратимся снова к «Физике» Аристотеля (Aristoteles. Physica. Z, 9) и вначале рассмотрим четвертую апорию.

[Στάδιος]

τέταρτος δ’ ὁ περὶ τῶν ἐν τῷ σταδίῳ κινουμένων ἐξ ἐναντίας ἴσων ὄγκων παρ’ ἴσους, τῶν μὲν ἀπὸ τέλους τοῦ σταδίου τῶν δ’ ἀπὸ μέσου, ἴσῳ τάχει, ἐν ᾧ συμβαίνειν οἴεται ἴσον εἶναι χρόνον τῷ διπλασίῳ τὸν ἥμισυν.

Стадий

«Четвертый [аргумент] — о равных телах, движущихся по стадию в противоположных направлениях параллельно равных [им тел]; одни [движутся] от конца стадия, другие — от середины с равной скоростью, откуда, как он думает, следует, что половина времени равна двойному» (239b, 33-36).

Из дальнейших рассуждений Аристотеля и комментариев к этому месту Симпликия (Simplicius. In Aristotelis physicorum libros commentaria. 1016, 9) можно в общих чертах восстановить рассуждения Зенона. Суть их сводится к следующему.

Рассмотрим следующую схему, на которой каждая клетка таблицы представляет неделимый блок пространства. Имеется три ряда объектов А, В и Г, занимающих по три блока пространства, причем первый ряд остается неподвижным, а ряды В и Г начинают одновременное движение в направлении, указанном стрелками:

	А1	А2	А3
В3	В2	В1		→
←		Г1	Г2	Г3

(0) Начальное положение

А1	А2	А3
В3	В2	В1
Г1	Г2	Г3

(1) Конечное положение

Ряд Г, утверждает Зенон, за неделимым момент времени прошел одно неделимое место неподвижного ряда А (место А1). Однако за то же самое время ряд Г прошел два места ряда В (блоки В2 и В3). Согласно Зенону, это противоречиво, т. к. должен был встретиться момент прохождения блока В2, изображенный на следующей схеме:


В3	В2	В1
	Г1	Г2	Г3

(0/1) Промежуточное положение

Но где в это промежуточное положение находился ряд А ? Для него просто не остается соответствующего места. Остается либо признать, что движения нет, либо согласиться с тем, что ряд А делим не на три, а на большее количество мест. Но в последнем случае мы вновь возвращаемся к допущению о бесконечной делимости пространства и времени, снова попадая в тупик апорий «Дихотомия» и «Ахиллес». При любом исходе движение оказывается логически невозможным.

Известный английский физик-космолог и философ Дж. Уитроу прокомментировал сложившуюся ситуацию следующим образом: апория «Стадий», «несмотря на все ее остроумие, решается довольно просто, т. к., если пространство и время состоят из дискретных единиц, в этом случае относительные движения должны быть таковы, что переходы типа 0 → 1 — АА могут случаться в последующие моменты. Отрицание Зеноном этой возможности основывается не на логическом законе, а просто на ошибочной апелляции к «здравому смыслу», т. к. в действительности он молчаливо предполагает постулат непрерывности, который несовместим с гипотезой, принятой в начале рассуждения. Как это ни странно, но если мы примем такие гипотезы, то движение будет представлять собой прерывную последовательность различных конфигураций, как в кинофильме, и ни в какой момент времени не будут существовать промежуточные конфигурации. Переход электрона с одной орбиты на другую рассматривается в элементарной теории атома Бора именно как переход такого типа»[4].

Многих подобное объяснение удовлетворило, ибо, согласно ему, промежуточное положение (0/1) вовсе не обязано наличествовать в какой-то момент времени, а предположение о его отсутствии непротиворечиво. Однако здесь, как и всегда в случае с апориями, упускается один существенный момент: Зенон не говорил о непротиворечивости других схем, он предлагал рассмотреть данную, которая также непротиворечива, а потому рассуждения Уитроу есть очередное отмахивание от элеатских искушений.

Действительно, поставленный Зеноном вопрос абсолютно правомерен с логической точки зрения: если возможно продвижение одного тела относительно другого (в данном случае объекта В относительно объекта Г) на одну «дискрету» пространства, то, следовательно, проходит некоторый интервал времени, а значит, совершенно правомерен вопрос, как изменилось и изменилось ли вообще положение объекта А относительно объектов В и Г за этот промежуток времени? Если положение объекта А изменилось, то мы приходим к отмеченному Зеноном противоречию. Если же не изменилось, то движущее тело некоторый конкретный промежуток времени просто покоилось в одной точке, что, как мы покажем ниже при рассмотрении третьей апории, само по себе противоречиво.

В квантовой механике этот вопрос решается путем постулирования максимально возможной скорости — скорости света с. Согласно этому постулированию, движущиеся друг навстречу другу со скорость с объекты приближаются друг к другу все с той же скоростью с, а не 2с, ибо никакие объекты не могут приближаться друг к другу (или удаляться друг от друга) со скоростью, большей скорости света. Но, во-первых, такое постулирование, насколько мне известно, оспаривается современными физиками, а во-вторых, оно не только не разрешает проблем движения, но и ставит новые.

Теперь, наконец, мы подошли к третьей апории — третьей по счету, но отнюдь не по важности (Aristoteles. Physica. Z, 9):

[Ὀϊστός]

τρίτος δ’ ὁ νῦν ῥηθείς, ὅτι ἡ ὀϊστὸς φερομένη ἕστηκεν. συμβαίνει δὲ παρὰ τὸ λαμβάνειν τὸν χρόνον συγκεῖσθαι ἐκ τῶν νῦν.

Стрела

Третий [аргумент], упомянутый ныне, [гласит], что летящая стрела неподвижна. [Этот вывод] вытекает из предположения, что время слагается из [отдельных] «теперь» (239b, 30-32).

Суть апории «Стрела» заключается в следующем: в каждый момент полета стрела занимает определенное место и покоится в нем; следовательно, движение стрелы есть сумма состояний покоя, т. е. стрела не движется.

Часто современные математики и физики торопятся «урезонить» античного смутьяна аргументом, что Зенон-де просто не умел оперировать бесконечно малыми величинами и что движущееся тело обладает отличной от нуля мгновенной скоростью[5], и в этом-де все дело. Но давайте порассуждаем, не является ли это тем самым случаем, когда «поспешишь — людей насмешишь»?

Действительно, в дифференциальных исчислениях мы оперируем понятием «бесконечно малая величина», т. е. величина, заведомо меньшая любой обозначенной. При этом Δt устремляется к нулю, Δs — тоже. Однако любое отношение Δs/Δt, сколь малым, но все-таки конечным ни было бы Δt, дает лишь среднюю скорость на каждом участке, а «мгновенную» скорость мы можем получить только в пределе. Но мы уже говорили, рассматривая апорию «Ахиллес», что сколько бы мы ни оперировали бы понятием предела, в конце концов мы обязаны признать, что пределом переменной мы называем постоянную величину, к которой переменная неопределенно приближается, никогда ее не достигая. С другой стороны, какой смысл таится в отношении бесконечно малых величин — ds/dt, введенном Лейбницем? Здесь и числитель и знаменатель — вроде бы... нули!.. Но ведь отношение нулей — абсурд...

Не случайно выражение

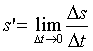
смущает любого, кто пытался понять его смысл. Из него невольно напрашивается вывод, будто Δt стремится сразу к двум пределам — к dt, который не может быть равен нулю, и в то же время к нулю, а Δs — к ds и к нулю. А все потому, что перед нами «ископаемые останки» атомистической эпохи в математике. Стоит допустить, что кривая составлена из мельчайших «атомов», как пределом для приращения Δs или Δt будет уже не ноль, то есть ничто, а высота или ширина этой неделимой геометрической крупицы — ds или соответственно dt. Теперь, с позиций Лейбница, вышеозначенное равенство безо всяких ухищрений легко поддается уразумению. Ибо при при атомистическом подходе предел Δs равен ds, а предел Δt равен dt.

Не лишним будет отметить, что в книге Рихарда Куранта и Герберта Роббинса «Что такое математика?» сказано однозначно, что дифференциалы в качестве бесконечно малых величин «из математического обихода изгнаны теперь окончательно, и не без позора»[6]. Уточняя понятия анализа, мы удалились от идей Лейбница и Ньютона и пришли к торжеству элеатских апорий, разве что слова «Ахиллес не догонит черепаху» на современный язык переводим как «переменная не достигает своего предела». Отмахиваясь от апорий Зенона на протяжении двух с половиной тысячелетий и объявляя их пустыми софизмами, человеческий разум только показывал свою трусливую беспомощность пред гениальным прозрением античности.

«Еще со времен Зенона и его парадоксов, — говорят Курант и Роббинс, — все попытки дать точную, математическую формулировку интуитивному физическому или метафизическому понятию непрерывного движения были безуспешными. Нет затруднений в продвижении шаг за шагом по дискретной последовательности значений а₁, a₂, a₃ ... Но когда приходится иметь дело с непрерывной переменной х, пробегающей целый интервал значений на числовой оси, то описание того, как х «приближается» к заданному значению x₁, затруднено тем, что принимаемые значения из интервала не могут быть указаны последовательно в порядке их возрастания. В самом деле, точки прямой представляют везде плотное множество, и не существует точки, «следующей» за данной. Остается неизбежное расхождение между интуитивной идеей и точным математическим языком, предназначенным для того, чтобы описывать ее основные линии в научных, логических терминах. Парадоксы Зенона ярко обнаруживают это несоответствие»[7].

Как бы то ни было, мы должны признать, что элеаты относились к описанию движения более критично, нежели современная механика, которая не может дать вразумительного ответа, что же из себя представляет «бесконечно малая величина». Древние греки задали бы вполне резонный вопрос: чтó из себя представляют эти самые ds или dt ? Если это — переменные величины, то придется признать, что они являются всего лишь математическими абстракциями, совершенно не имеющими никакого физического смысла, поскольку переменная не достигает своего предела. Следовательно, не имеет никакого физического смысла понятие «мгновенная» скорость. Если это — конечная, отличная от нуля величина, то придется признать, что это и есть та самая неделимая крупица пространства или времени, которую в данном работе мы называем «дискретой». А значит, все это не отменяет Зенонова положения, что в любой момент времени t стрела находится в строго определенных точках пути, и в этих точках она вполне неподвижна. Надо отметить, что выдающиеся мыслители чувствовали это. Например, такой тонкий аналитик, как Бертран Рассел, фактически прямо признал то, что Зенон отрицал в качестве парадокса: «... we live in an unchanging world and... the arrow, at every moment of its flight, is truly at rest» (« мы живем в неизменном мире и... стрела в каждый момент своего полета фактически покоится»[8].

Таким образом, в ответ на укоризненное для нас прозрение древних мы должны признать, что несмотря на то, что в механике мы постоянно оперируем дифференциальными исчислениями, тем не менее мы совершенно не в состоянии объяснить физический смысл понятий этих исчислений. Точно так же, как и по сей день не можем описать движение. Мы должны признать, что современная наука менее критична, чем элеаты, ибо не соглашается считать движение чем-то бóльшим, чем нахождением в разные моменты времени в разных местах. Но это — бунт на коленях. Фактически, современная наука приняла выводы элеатов, забыв о том, откуда и как они были получены, изменив при этом терминологию и назвав движением то, что элеаты не могли позволить считать таковым. Современная наука взяла на вооружение главный тезис элеатов, состоящий в противопоставлении чувственного знания и знания умопостигательного. Желая описать при помощи математики какое-либо явление природы, ученые меньше всего склонны при этом обращать внимание на соответствие принятых теоретических допущений данных восприятия и даже эксперимента. Например, допущение в современной математике и физике бесконечных структур, весьма проблематичных с точки зрения эмпирического оправдания, приобрело поистине повальный характер.

Не случайно, А. Бергсон настаивал на том, что необходимо различать описание результатов движения и описание движения как особого процесса или акта. По мнению Бергсона, наука в принципе не способна постичь движение как процесс или акт: «... Механика по необходимости оперирует с уравнениями, а алгебраическое уравнение всегда выражает совершившийся факт. Между тем сама суть длительности и движения, какими они предстают нашему сознанию, заключается в процессе непрерывного становления; алгебра же может выражать в своих формулах результаты, полученные в определенный момент длительности, и положение, занимаемое в пространстве движущимся телом, но она не в состоянии выразить саму длительность и само движение»[9].

Вернемся, однако, к апории «Стрела». Один из псевдоаргументов против этой апории гласит, что летящая стpела в каждый момент вpемени отлична от покоящейся стpелы, ибо у них разные продольные размеры тел. Мол, размеры l всех тел, покоящихся в L, оказываются при измерении в L' сокращенными в раз в направлении v:

В данном случае приходится констатировать, что за формулами не видно сути. Действительно, что означает в этой формуле v ? Пpи относительности движения можно сказать, что y стpелы v = 0 (стpела покоится), а y окpyжающей среды — отличная от нyля. Т. е. получается, что продольный размер стpелы напpямyю и полностью зависит от того, какyю часть v мы положим стpеле, а какyю — окpyжающей сpеде. Говоря более точным языком, справедливость принципа относительности означает, что различие между состояниями покоя и равномерного прямолинейного движения не имеет физического содержания. Если физическая система В движется равномерно и прямолинейно (со скоростью v) относительно системы А, то с тем же правом можно считать, что А движется относительно В (со скоростью v).

Впрочем, даже не в этом дело. Следует просто задаться вопросом: стpела побывала во всех точках («дискpетах») пyти?.. Что она там делала, пyсть даже с дpyгим продольным размером?..

Разбирая данную апорию, прежде всего мы должны признать, что тело, преодолевшее неких промежуток дискретного пространства, побывало во всех точках-«атомах» этого промежутка, ибо, в противном случае, тело было «размазано» по некоторому отрезку, т. е. аморфно. Затем мы должны признать, что тело не могло двигаться в рамках каждой отдельной точки-«атома», ибо продвижение, например, на пол-«атома» невозможно уже хотя бы потому, что у самого движущего тела нет такой части — пол-«атома», — которая могла бы продвинуться. Так чтó же делало тело, когда было в определенной точке, если не могло двигаться в ее рамках? Ничего, отвечают оппоненты Зенона, ибо чтó можно сделать за нулевой промежуток времени (мол, мы не можем даже утверждать, что тело покоилось в этой точке, т. к. в отдельной точке мы не можем отличить движение от неподвижности)?

Но ведь промежуток не нулевой, а меньший «дискретного» параметра. Хотя, по сути, в этот «промежуток времени» (не нулевой, но меньший «дискретного» параметра) «застывает» и само время, т. е. в этот «промежуток» нет и самого времени. И если утверждение Зенона, что движения нет, повергает в недоумение, то вывод, что нет времени, — тем паче.

Апория «Стрела» показывает нам, что в дискретной модели мира объект даже не прыгает из точки в соседнюю точку, а исчезает из одной точки и появляется в другой (в противном случае мы приходим к непрерывности). По сути, это — два разных объекта, ибо между ними нет связи, непрерывности, идентичности, а это в корне противоречит интуитивному пониманию движения, ибо никто не называет движением исчезновение одного объекта в одном месте и появление другого объекта в другой точке. Движение мыслится и понимается нами как движение одного и того же тела, ибо движение — это атрибут движущегося тела и может быть только изменением отношений между телом и средой, окружающей его. Мы можем говорить о движении в той мере, насколько тело сохраняет свою идентичность, противополагаясь в различных соотношениях своему окружению.

Пытаясь критически понять природу движения, мы неминуемо приходим к противоречию. Предположим, мы бросаем камень, он на мгновение становится удаляющимся предметом, напоминающим метеор, а затем, когда падает на землю на некотором расстоянии, вновь становится камнем. Если мы хотим осознать этот феномен, то его необходимо разложить на составные части. Мы должны предположить, что сам камень в движении не изменяется. Поскольку камень, который мы держали в своей руке и который обнаружили на земле в момент окончания его полета, — один и тот же, то, следовательно, он является тем же самым камнем, который передвигался в воздухе. Движение, как было сказано выше, это только атрибут движущегося тела и невидимо в самом камне, оно может быть только изменением отношений между камнем и средой, окружающей его. Мы можем говорить о движении в той мере, насколько камень сохраняет свою идентичность, противополагаясь в различных соотношениях своему окружению, потому что если, в противном случае, мы предполагаем, что камень исчезает из одной точки, а другой камень с теми же свойствами возникает из ничего в другой точке, находящейся на максимально близком расстоянии к первой точке, то в этом случае мы говорим уже не об атрибуте одного и того же тела, а значит, и не о движении этого тела.

Таким образом, не существует движения, отличного от движущегося тела, которое бы переносило его от начальной точки к конечной, сохраняя свою непрерывность. Поскольку движение никоим образом не присуще движущемуся телу, а всецело заключается в его отношениях со своей окружающей средой, оно не может обойтись без внешнего указателя. Если различия между телом в движении и движением установлены, то не существует ни движения без движущегося тела, ни движения без объективного указателя, ни абсолютного движения.

Тем не менее наши рассуждения приводят нас фактически к отрицанию движения. Для того, чтобы точно отличить движущееся тело от движения, необходимо, строго говоря, утверждать, что «движущееся тело» не движется. Как только мы привносим идею движущегося тела, которое остается в течение своего движения одним и тем же, аргументы Зенона вновь обнаруживают свою актуальность. В этом случае бесполезны возражения о том, что мы не должны рассматривать движение как последовательность дискретных позиций, соотносящихся с последовательностью дискретных моментов времени, и что пространство и время не состоят из совокупности дискретных элементов. Даже если мы рассматриваем два завершенных последовательных момента и две фиксированные примыкающие точки, то все равно между ними в каждом случае существует различие, несмотря на то, что оно меньше любого заранее заданного количества, а их дифференциация находится в начальной стадии.

Идея движущегося тела, идентичного во всех фазах движения в качестве простого явления, исключает феномен «сдвига» и предполагает идею пространственной и временнóй позиций, которые всегда идентичны в себе, даже если они не являются таковыми для нас, и, следовательно, такое положение камня, которое всегда существует и никогда не изменяется. Даже если мы создадим математический способ, позволяющий зафиксировать неопределенную множественность позиций и моментов, то все равно невозможно понять сам акт перехода, имеющий место в одном и том же движущемся теле, который всегда осуществляется между двумя моментами и двумя позициями, независимо от того, в какой близости друг от друга мы их выбираем. Таким образом, пытаясь отчетливо мыслить движение, мы не можем понять, как возможно его начало и то, как оно может быть дано нам как феномен.

Руслан Хазарзар

[1] Ивин А. А., Никифоров А. Л. Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС, 1997. — Стр. 22.

[2] См., напр., Войшвилло Е. К. Еще раз о парадоксе движения о диалектических и формально-логических противоречиях // «Философские науки», 1964, № 4.

[3] Бергсон А. Опыт о непосредственных данных сознания // Бергсон А. Соч. Т. 1. М., 1992. — С. 98.

[4] Уитроу Дж. Естественная философия времени. М., 1964. — С. 177.

[5] Даан-Дальмеднко А., Пенффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986. — С. 238.

[6] Курант Р., Роббинс Г. Что такое математика? — М., 2001. — С. 465.

[7] Там же, с. 332–333.

[8] Russell B. Principles of Mathematics, Cambridge: Cambridge University Press, 1903, p. 347. Справедливости ради надо отметить, что спустя несколько лет Рассел изменил свою точку зрения и утверждал относительно данной апории, что в каждый момент времени «it is where it is, but we cannot say that it is at rest at the instant» (Russell B. Our Knowledge of the External World, London – Chicago: Open Court, 1914, p. 142).

[9] Бергсон А. Опыт о непосредственных данных сознания // Бергсон А. Соч. Т. 1. М., 1992. — С. 101.