Костенко И.П.
Коренная причина падения качества отечественного математического образования
Оценки показателей качества. Главной характеристикой качества математического образования является качество знаний учащихся и, прежде всего, выпускников общеобразовательной школы. Для количественной оценки этого показателя мы используем процент отличных и хороших отметок проверочных работ (экзаменов, тестов) в различных выборках и называем такую оценку кратко качеством-1. Процент отличных, хороших и удовлетворительных отметок, который официально называется “процентом успеваемости”, мы называем качеством-2. Эти проценты до 1970-х гг. оцениваются приближённо (они показаны на рис. 1) путём сопоставления разных данных (результаты массовых официальных контрольных работ, тестов, вступительных экзаменов в вузы, международных исследований, экспертные оценки учителей, методистов, преподавателей высшей школы) и учитывая их согласованность между собой.
После реформы, со второй половины 1970-х гг., трудность экзаменационных заданий и требования к отметкам стали резко снижаться. С этого времени мы не можем достоверно оценить введённые показатели. Но можем установить тенденции их изменения, в частности, по решаемости базовых типов заданий.
Поясним две оценки. Наиболее достоверная оценка сделана по результатам глобальной проверки знаний, проведённой методическим Сектором АПН в 1949 г. в 14 областях РСФСР. Сектором проанализированы 14193 работы и результаты отражены в таблице,[1] из которой мы и вывели оценку качества-1 в 74%, взяв среднее значение процентов хороших и отличных решений разного типа заданий по трём математическим предметам учениками IX-X классов.
Оценка качества-1 2009 г. сделана по выборке первокурсников МАДИ, прошедших контрольное ЕГЭ-тестирование, проведённое преподавателями института.[2] Этот процент (2,4%) согласуется с результатами ЕГЭ по стране: «доля выпускников с хорошими (более 75) и, тем более, отличными (более 90) баллами ничтожно мала». [3] Процент МАДИ согласуется с результатами международного тестирования PISA-2009, – «продвинутым математическим мышлением и умением проводить рассуждения» обладают 3,6% наших 15-летних школьников.[4]
Общая картина динамики качества знаний за 80 лет показана на рис. 1. Диаграмма представляет, в сущности, вероятностную модель изменения этого качества. Сделаем необходимые пояснения.
Ломаные построены по узловым точкам, соответствующим узловым годам, для которых удалось обоснованно определить оценки показателей качеств-1 и 2 (с 1937 до 1970 г.) и динамику их изменения (до 1937 г. и после 1970 г.). Ломаные не являются графиками изменения этих показателей, – они совпадают с графиками в узловых точках, а между этими точками представляют линейные приближения хода графиков. Поэтому мы называем эти ломаные тенденциями. Поскольку до 1937 г. и после 1970 г. мы не имеем необходимых оценок качеств-1 и 2, ход этой части тенденций показан пунктиром. Из рис. 1 видно, что возможные колебания оценок не влияют на направленность тенденций и, практически, на их скорость.
Начинается диаграмма с 1931 г., поскольку статистических данных для того, чтобы оценить показатели качества знаний выпускников школ 1920-х гг., нет. Период 1918 – 1931 гг. это период первой "коренной” реформы школы, “слома” традиций, поиска “инновационных” форм и методов обучения в идеологических рамках мифической “трудовой школы”. Этот “поиск” привёл к полной хаотизации всей системы образования и к падению качества знаний учащихся почти до нуля (как и сегодня).
Этот факт имеет официальное подтверждение: в 1930 г. «Главсоцвос указывал, что … ни с количественной, ни с качественной сторон знания поступающих не соответствуют тем минимальным требованиям, которые к ним предъявляются. Сплошь и рядом наблюдается отсутствие навыков в обращении с простыми и десятичными дробями, в преобразовании алгебраических формул, в составлении уравнений и решении геометрических задач и т. д.».[5]
Первичный анализ диаграммы. Видим, что весь 80-летний промежуток делится на три периода: 1) 1931-1956 гг. – рост качества; 2) 1956-1978 гг. – падение качества; 3) 1978-2009 гг. – сползание качества практически до нуля.
Первый период делится на три части:
- 1931-1937 гг. – резкий рост качеств-1 и 2 до приемлемого высшей школой уровня.
- 1937-1949 гг. – продолжение того же среднего темпа роста качества-1 и значительное замедление роста качества-2.
- 1949-1956 гг. – стабилизация качества-1 и небольшой рост качества-2, достижение максимума качества – 74-82%.
Второй период тоже делится на три части:
- 1956-1960 гг. – резкое падение качества-1 (в 3,5 раза) и качества-2, вызванное первым вторжением «реформаторов» в программы и методы обучения.
- 1960-1970 гг. – стабилизация качества-1 и продолжение падения качества-2 с некоторым замедлением, в результате приспособления учителей к новой программе и учебникам.
- 1970-1978 гг. – обвальное падение качеств-1 и 2 в результате реформы.
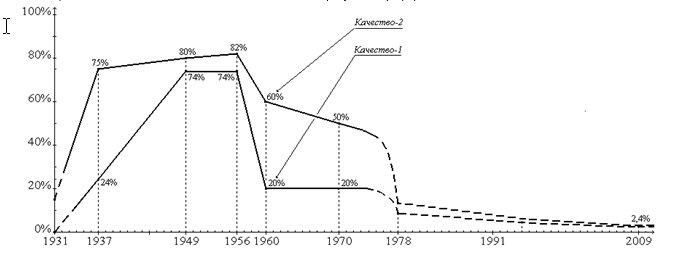
Рис. 1. Тенденции изменения качества математических знаний школьников с 1931 по 2009 г.
Третий период можно разделить на две части:
- 1978-1991 гг. – продолжение падения качеств-1 и 2 примерно в два раза.
- 1991-2009 гг. – стабилизация качеств-1 и 2 почти на нулевом уровне.
Далее кратко охарактеризуем все три периода и сосредоточимся на втором периоде 1956–1978 гг.: определим факторы управленческой политики и методические идеи, внедрение которых в учебный процесс общеобразовательной школы вызвало падение качества. Тем самым будут вскрыты истинные и глубинные причины нынешней деградации нашего математического образования.
1931-1937 гг. – период непрерывного и быстрого роста качества математического образования и качества знаний выпускников школ страны. Он проходил под знаком жёстко поставленной государством перед школой задачи «подготовки для техникумов и для высшей школы вполне грамотных людей, хорошо владеющих основами наук».[6] Задача эта была решена в фантастически короткий срок – за 6 лет. И решена не на пути поиска «инноваций», а на пути возврата к традиции. Были восстановлены организационные формы и методические принципы обучения русской гимназии. Введена предметная система обучения. Систематизированы, облегчены и сделаны стабильными учебные планы и программы. Восстановлен принцип единого стабильного учебника (Киселёв-Рыбкин). Повышена требовательность к оценке знаний учащихся и установлены единые нормы оценки.[7] Поднят престиж учителя и повышена его зарплата до средней по промышленности. Ужесточена ответственность управленцев всех звеньев. Проследить более детально за тем, как решалась эта ключевая государственная задача, можно по Постановлениям ЦК 1931–1936 гг.[8]
А вот как работники Наркомпроса выполняли эти Постановления. Они ежегодно проводили массовые, выборочные, всесторонние обследования школ страны. Во время проверок проводились письменные контрольные работы по всем предметам. Анализ работ с выявленными типичными ошибками, объяснениями их причин и методическими рекомендациями по их исправлению (!!) оперативно рассылался учителям в виде методических писем. На следующий год показатели школ сравнивались с предыдущими.[9]
В результате грамотной дружной работы учителей, методистов и управленцев государственная задача поднятия качества образования была к 1937 г. решена. Директор МЭИ И. И. Дудкин: «В текущем году средняя школа дала значительно лучше подготовленную молодёжь, чем в 1936 г. Это подтверждается материалами приёмных испытаний».[10] Этот вывод делают и другие вузы, не только московские: «В целом подготовка выпускников десятилеток в этом году несравненно выше, чем в 1935 и 1936 гг».[11] Анализ количественных результатов приёмных испытании 1937 г.[12] позволяет сделать оценки качества-2 – 24%, качества-1 – 75%, что и отражено на рис. 1.
1937-1956 гг. – продолжение роста качества. В разгар войны, 11 августа 1943 г., был принят закон о повышении заработной платы учителям. За один военный год к 1944 г. фонд заработной платы увеличился почти в 2 раза.[13] Общие ассигнования на народное просвещение за годы войны увеличились более, чем в 1,5 раза.[14]. Эти факты проявляют приоритетность образования в государственной политике даже во время войны.
21 июня 1944 г. вышло Постановление СНК СССР «О мероприятиях по улучшению качества обучения в школе». Между прочим, в этом Постановлении осуждалась процентомания. 15 августа 1944 г. нарком В. П. Потёмкин провёл Всероссийское совещание, посвящённое «проблеме улучшения качества обучения и воспитания нашей молодёжи».[15] Через год на таком же августовском совещании 1945 г. нарком поставил тот же вопрос – «о дальнейшем улучшении учебно-воспитательной работы в школе». Коренным недостатком в знаниях учащихся, по заключению совещаний, является формализм. Средства преодоления, опять же, не инновационные, а традиционные: «укрепление знаний учащихся путём систематического повторения и регулярной проверки».[16] Причём «повторения с учащимися пройденного материала как за курс данного года обучения, так и за предшествующие классы».[17] Другое средство – «улучшение контроля за работой школ и учителей и постановки учёта знаний учащихся».[18] Контроль не надзирающий, а помогающий.
Методический принцип регулярной проверки знаний будет упразднён «реформаторами» в конце 1950-х гг. под тем предлогом, что он занимает слишком много времени урока, в то время как новые «активные» методы обучения требуют, чтобы учащиеся усваивали новый материал на самом уроке. Одновременно упразднялись домашние задания, которые воспитывали привычку к самостоятельному труду. Так разрушалась классическая методика организации урока, восстановленная В. П. Потёмкиным.
Через 3 года проблема формализма в знаниях была в значительной мере решена. Проф. МГУ П. С. Моденов: «Приёмные испытания (1947 г. – И.К.), … свидетельствуют о положительных сдвигах в подготовке учащихся средней школы по математике за последний год (заметное улучшение только за один год! – И.К.). … Многие из предложенных задач были блестяще решены абитуриентами. Это ещё раз свидетельствует о том, что в наши вузы идёт талантливая и в большинстве своём отлично подготовленная молодёжь».[19]
Через 9 лет, в 1956 г. методист П. В. Стратилатов в статье, обобщающей опыт проведения экзаменов 1955 г. в средних школах, заключает: «… знания учащихся по математике постоянно повышаются. Это отмечают все авторы статей и материалы инспекторских обследований работы школ».[20]
Заметим, – после 1956 г. мы никогда и ни от кого не услышим подобных оценок.
Второй период 1956–1978 гг. проходит под знаком менее чётко, но не менее жёстко поставленной другой задачи, озвученной профессором математики А. И. Маркушевичем в докладе на сессии АПН в 1949 г.: «повысить идейно-теоретический уровень преподавания математики в средней школе».[21] Эта задача подменила задачу «улучшения качества обучения» и предопределила обратный процесс выведения из обучения классических принципов методики, разрушения выверенных длительным опытом программ и уничтожения понятных учебников.
Процесс этот незаметно начат в 1949 г., когда в Объяснительную записку к программе было вставлено: «программа по арифметике, не исключая совершенно решение типовых задач, отводит им довольно скромное место, учитывая, что в дальнейшем типовые задачи более сложных видов учащиеся будут решать методом составления уравнений».[22] В VI классе в курсе алгебры «рекомендуется, начиная с первой (?!) темы “Буквенные обозначения”, решать уравнения и задачи на составление уравнений».[23]
Эта «скромная» рекомендация положила начало разрушению классической методики обучения решению задач (сначала типовых арифметических) и блокировке развития мышления учащихся. Через десять лет, к началу 1960-х гг. учителя констатировали, что выпускники школ «совершенно не умеют решать арифметических задач, а прибегая к решению их алгебраическим путём, часто допускают ошибки в составлении уравнений».[24]
В 1956 г. «реформаторами» был сделан второй решающий шаг, – из школы-семилетки выведены учебники Киселёва, а из 10-го класса учебник Рыбкина. И уже в следующем 1957 г. министерская проверка фиксирует заметное падение качества знаний.[25] Новые малопонятные учащимся учебники, что отмечали все учителя,[26] нарушили главное условие формирования качественных знаний – самостоятельную работу с книгой, самостоятельное осмысление знаний.
Одновременно «реформаторы» начали разрушение классической организации урока. Они потребовали от учителей ликвидировать проверку домашней работы учащихся и поставили неразрешимую задачу – чтобы материал урока был усвоен учащимися на самом уроке. В результате, учащиеся перестали выполнять домашние задания, перестали самостоятельно работать дома, что привело к дальнейшему падению качества знаний и ослаблению навыков.
В конце 1950-х гг. в Министерство стали поступать «жалобы вузов на недостатки знаний поступающих».[27]. И к 1960 г. качество-1 упало до 20 %, в 3,5 раза. Заключение вузовских преподавателей: «хорошо подготовлена лишь пятая часть поступающих в вузы, процентов 40 имеют удовлетворительные знания, остальные не подготовлены».[28]
Третий шаг – принятие в 1960 г. новой программы, новые принципы которой: изучать десятичные дроби до (?) обыкновенных; разгрузить алгебру от сложных задач и примеров; упразднить (?) отдельный курс тригонометрии; усилить «функциональную направленность курса алгебры»; внедрить высшую математику (производная и её приложения); усилить дедуктивность и логику в геометрии.[29]
Результаты этих новаций оценивают вузовские преподаватели: «Основные недочёты в знаниях: формализм, слабая логическая подготовка, отсутствие необходимых навыков в тождественных преобразованиях».[30]
А теперь сопоставим результаты с реформаторскими новациями: «реформаторы» перестроили арифметику, результат – падение вычислительных навыков. Упразднили цельный курс тригонометрии, – «неблагополучие» с тригонометрическими навыками. Усилили функциональную пропедевтику, – выпускники не знают элементарных функций, их свойств и графиков. Ввели производную, – «никто (!) не мог дать определения предела». Повысили теоретический уровень учебных предметов, – ученики перестали их понимать, усилился формализм знаний, ослабла логическая подготовка.[31]
Десятилетие 1960-х гг. проходит для школы относительно стабильно, что позволяет учителям как-то приспособиться к новым программам и учебникам и сохранять допустимый уровень математических знаний учащихся. Качество-2 продолжает снижаться и к концу 1960-х гг. опускается до 50 %: в 1969 г. в МГПИ «на письменной работе по математике было отсеяно около половины поступающих».[32] Такие же результаты в МГУ и в других, в том числе нестоличных вузах.
«Реформаторы» игнорируют результаты «перестройки» (именно так называл А. И. Маркушевич и другие «реформаторы» то, что они делали со школой за пятилетие 1956 – 1960 гг.; любопытна аналогия с пятилетней горбачёвской «перестройкой») и продолжают настойчивую идеологическую и организационную подготовку задуманной ими ещё в 1930-х гг. реформы. Процесс зарождения идей реформы, её подготовки, реализации и закрепления результатов раскрыт в другой статье автора.[33]
Основные идеи реформы принадлежат отнюдь не А. Н. Колмогорову, все они были сформулированы А. Я. Хинчиным в 1939 г.:
- «Самой категорической (?) необходимостью является введение в школьные программы оснований анализа бесконечно малых».[34]
- «Программы должны быть построены так, чтобы идеи переменной величины и функциональной зависимости … как можно ранее усваивались учащимися и … становились основным стержнем всего школьного курса математики».[35]
- Повысить строгость «отчётливых и точных определений, формулировок и рассуждений», соответствующих «современной науке».[36]
- «Исключить из основного материала арифметики пятого класса» задачи, «которые … представляют собой … алгебраические задачи на составление уравнений».[37]
Все эти и все другие реформаторские идеи противоречат классическим законам дидактики («от простого к сложному», «от конкретного к абстрактному», «от известного к неизвестному» и др.). Все их идеи не учитывают возрастных особенностей мышления детей. В частности, формулировки и рассуждения в школьном учебном курсе должны соответствовать прежде всего возрастным возможностям детей, а не «современной науке». Порочность всех реформаторских идей сразу же доказала ПРАКТИКА, жизнь.
1970–1978 гг. – реализация реформы-70 (будем так её называть), слом всей методической системы отечественного образования, коренное изменение программ и учебников. Результат – обвальное падение качества знаний. Свидетельствует непосредственный участник реформы, академик РАО Ю. М. Колягин:
«Всё встало на свои места при первом выпуске (в 1978 г. – И.К.) из средней школы “отреформированной” молодёжи, … среди учёных-математиков АН СССР и преподавателей вузов началась паника. Было повсеместно отмечено, что математические знания выпускников школ страдают формализмом; навыки вычислений, элементарных алгебраических преобразований, решения уравнений фактически отсутствуют. Абитуриенты оказались практически не подготовленными к изучению математики в вузе».[38]
Третий период 1978–2009 гг. – годы закрепления результатов реформы-70 и сползания качества знаний до нуля. Все эти годы все недостатки, проявившиеся после реформы (формализм, логика, навыки) не исправлялись, а сохранялись и усугублялись. Потому что «реформаторам» удалось под видом «совершенствования» «порочных» программ и «недоброкачественных» учебников (оценки Президиума ОМ АН СССР) удержать все свои основные идеи: «интегрированные» учебные курсы вместо цельных учебных предметов, суррогат высшей математики в программах, их запредельная перегруженность, аксиоматика, схоластический формализм и абстрактность изложения в учебниках.
Сравнительный анализ (с 1981 по 1988 гг.) решаемости базовых экзаменационных заданий, проведённый преподавателями МАДИ, показал падение качества-2 почти в два раза.[39] То же подтверждали другие вузы.[40] В 2013 г. результаты ЕГЭ по всей стране дают оценку качества-1 менее 1 %.[41]
Сегодня фиксируется незнание студентами таблицы умножения, площади круга, параллелограмма, неспособность складывать дроби и пр. Разлагаются те крохи знаний, которые раньше имели «двоечники». Поэтому этот период можно назвать гниением нашего образования. К методическим факторам, запущенным реформой-70, добавились социальные и организационные – непрерывная дестабилизация работы учителей и её обессмысливание «процентоманией», разрушение дисциплины и труда учащихся идеей свободы личности, навязывание школе ложных целей и методов (компьютеризация, информационные технологии, «развивающие» методики обучения, «вариативные» учебники, ЕГЭизация «компетентностный подход» и пр., и пр.), рост бюрократизации и поддержание хаотизации непрерывной сменой установок, требований, форм отчётности, и пр., и пр., и пр.
Реформа-70 отдаляется и отдаляется. И мы забываем, что обвальная деградация началась с этой реформы, и её идеология – исходная, коренная причина непрекращающегося вот уже почти 60 лет падения качества математического образования (и школьного, и вузовского). Ложный принцип этой реформы, – повышение научности, а на самом деле, псевдонаучности обучения, – изгнал из учебников педагогику и методику, изгнал Ученика. Он ответствен за деградацию мышления, а значит, и личности учащихся. Именно он привёл учащихся к массовому отвращению от учёбы. Он породил государственную ложь (так называемую «процентоманию»), которая заблокировала все возможности исправления ситуации. Он запустил прогрессирующую коррупцию в сфере образования. До сего дня наша школа живёт под тяжким бременем этой реформы. И мало кто помнит и понимает истоки сегодняшних бед. Но забыв прошлое, не понимая истинных причин и движущих сил, глупо надеяться на будущее.
[1] О преподавании математики в V-X классах. М, 1949. С. 6.
[2] Математика в школе. 2010. № 2. С. 42.
[3] Там же. С. 57.
[4] Математика в школе. 2011. № 3. С. 69.
[5] Милюков П. Н. Очерки по истории русской культуры. Т. 2, ч. 2. М, 1994. С. 130.
[6] Народное образование в СССР: Общеобразовательная школа: Сб. документов 1917-1973 гг. М., 1974. С. 157.
[7] Нормы оценки успеваемости учащихся по математике. М., 1943.
[8] Народное образование в СССР: Общеобразовательная школа: Сб. документов 1917-1973 гг. М., 1974.
[9] Материалы Всероссийского совещания преподавателей математики средней школы, март-апрель 1935. М., 1935. С. 14-16.
[10] Высшая школа. 1937. № 10. С. 41.
[11] Там же. С. 48.
[12] Там же. С. 41, 48. Высшая школа. 1936. № 2. С. 13-17.
[13] Потёмкин В. П. Статьи и речи по вопросам народного образования. М., 1947. С. 186.
[14] Там же. С. 243.
[15] Там же. С. 190.
[16] Там же. С. 212–213.
[17] Там же. С. 254.
[18] Там же. С. 190.
[19] Математика в школе. 1948. № 2. С. 15.
[20] Математика в школе. 1956. № 2. С. 17.
[21] Математика в школе. 1950. № 1. С. 1.
[22] Математика в школе. 1949. № 6. С. 5.
[23] Там же, с. 6.
[24] Математика в школе. 1964. № 1. С. 58.
[25] Математика в школе. 1958. № 6. С. 91.
[26] Математика в школе. 1957. № 4. С. 41, 42, 47, 57.
[27] Маркушевич А. И. Об очередных задачах преподавания математики в школе // На путях обновления школьного курса математики / Состави тели: А. И. Маркушевич, Г. Г. Маслова, Р. С. Черкасов. – М. ,1978. С. 38.
[28] Математика в школе. 1961. № 4. С. 15.
[29] Математика в школе. 1959. № 1. С. 41–51.
[30] Математика в школе. 1961. № 4. С. 15.
[31] Там же. С. 19 – 29.
[32] Математика в школе. 1971. № 2. С. 61.
[33] Костенко И. П. Корни, ветви и «ягодки» реформы-70 / Математическое образование. 2009. №2 (50). С. 14 – 23.
[34] Математика в школе. 1939. № 6. С. 1.
[35] Там же. С. 2.
[36] Математика в школе. 1939. № 4. С. 4.
[37] Математическое просвещение. М., 1961. № 6. С. 35.
[38] Колягин Ю. М. Русская школа и математическое образование. М., 2001. С. 200.
[39] Математика в школе. 1989. № 2. С. 57.
[40] Там же. С. 42 – 43.
[41] Математика в школе. 2013. № 7. С. 33.
22.11.2014